ベルヌーイ数とその周辺の数学

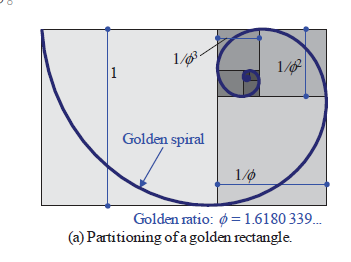
べき級数の展開係数としてベルヌーイ数を導入し, ベルヌーイ数の特徴を 調べていきます。その結果として, ベルヌーイ数が漸化式で計算できる 有理数であることを導きます。

• べき級数を一般化することでベルヌーイ数が導入できる。
• ベルヌーイ数は有理数である。
• ベルヌーイ数の一般項は二重級数で表現できる。

ベルヌーイ数と関連がある数列としてスターリング数を紹介します。 スターリング数には, 第1種スターリング数と第2種スターリング数があり, ともに, 組み合わせ論で意味をもつ数列です。 それらの数列は, 導入の時点では, 上昇階乗と下降階乗 (PDFファイル参照) と いう概念を用います。スターリング数はベルヌーイ数の一般項を 記述する手段として使うことができます。

• 上昇階乗と下降階乗について。
• スターリング数 (第1種と第2種) の導入。
• スターリング数とベルヌーイ数の関係。
• 組み合わせ論におけるスターリング数の意味。

ベルヌーイ数は正接関数 (tan x) と正割関数 (sec x) の ローラン展開における展開係数と密接な関係があります。 正接関数の展開係数としてタンジェント数を, 正割関数の展開係数として オイラー数を導入し, それらとベルヌーイ数の関係を調べていきます。

• 正接関数の級数展開とベルヌーイ数の関係。
• 正割関数の級数展開からセカント数の導入。さらに, オイラー数を定義する。
• タンジェント数とセカント数は規則的な一つの数列にまとめられる。

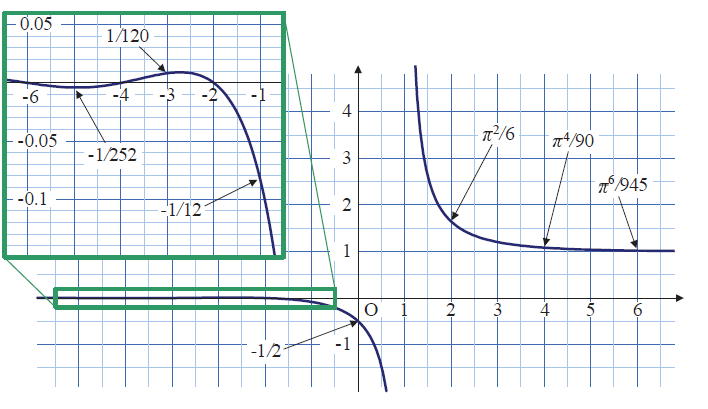
高次の調和級数をゼータ関数 ζ(s) として定義します。 ゼータ関数は, 素数と関連があり, さらに, 物理学における超弦理論の臨界次元を決める方程式に現れるなど, さまざまな分野で現れます。興味深いことに, 偶数ゼータ関数 ζ(2n) はベルヌーイ数と 円周率を用いて厳密値が計算できます。 一方, 奇数ゼータ関数 ζ(2n + 1) は厳密値の表記が見つかっていません。

• 調和級数とオイラー定数 γ の関係。
• バーゼル問題: 2次の調和級数は π²/6 に収束する。
• ゼータ関数の導入。偶数ゼータ関数はベルヌーイ数と円周率で記述できる。
• ゼータ関数の解析接続。 1 + 2 + 3 + 4 + ··· = -1/12 ???

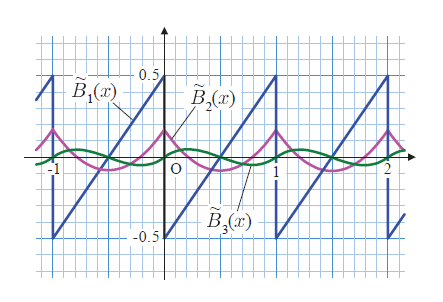
ベルヌーイ数とオイラー数を展開係数とする多項式を定義すれば ゼータ関数が容易に評価できるようになります。 さらに, それらの多項式は次章で取り扱う和公式につながっていきます。

• ベルヌーイ多項式とオイラー多項式の導入。
• 周期ベルヌーイ多項式と周期オイラー多項式の導入。
• ベルヌーイ多項式によるべき乗和の再考察。
• オイラー多項式によるゼータ関数の再考察。

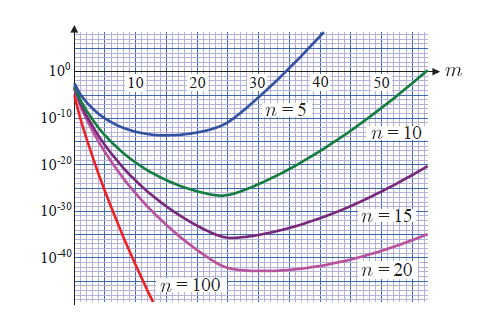
関数の形をした級数を計算する手法として, オイラー・マクローリンの総和公式と オイラー・ブールの総和公式を紹介します。それらの公式の導出には, 前章で取り扱った多項式が役に立ちます。得られた和公式を利用し, オイラー数が計算できるようになります。

• オイラー・マクローリンの和公式を利用し, スターリングの公式を導出。
• オイラー・マクローリンの和公式を利用し, オイラー数を計算。
• 発散級数 1 + 2 + 3 + ··· と ζ(-1) との関係。
• オイラー・ブールの和公式を利用し, ライプニッツ級数の誤差を考察

• 微積分の公式 [PDF]
• 部分分数展開 [PDF]
• 第2種スターリング数の一般項 [PDF]
• 負整数のゼータ関数の考察 [PDF]