楕円積分と楕円関数

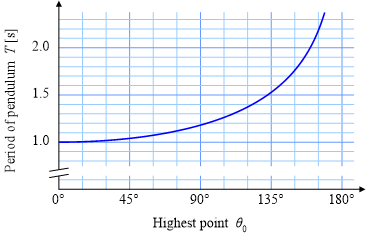
楕円積分を三つのタイプに分類し, 振り子の周期や円環ポテンシャルの 問題に対して楕円積分を実行します。

• 振り子の周期は厳密には一定ではない。
• 第1種楕円積分と第2楕円積分は, 算術幾何平均で高速計算できる。
• 楕円の周囲長は第2種楕円積分で計算できる。

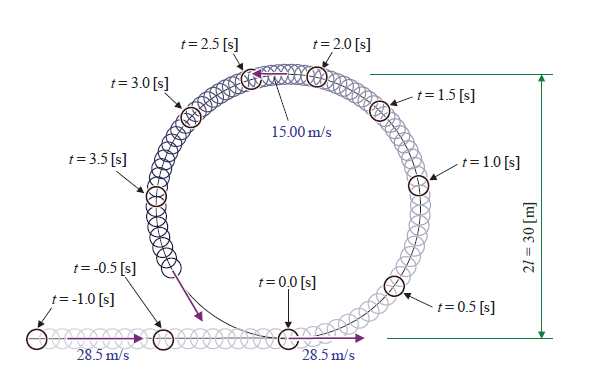
楕円積分の逆関数としてヤコビの楕円関数が定義されます。 定義域を実数全体に拡張すると, 楕円関数は周期関数です。 本章ではヤコビの楕円関数の性質を調べます。

• 母数 k が小さければ, 楕円関数は三角関数に近い。
• 振り子の運動や, ローラコースターの位置は時間の関数として書くと ヤコビの楕円関数で記述できる。

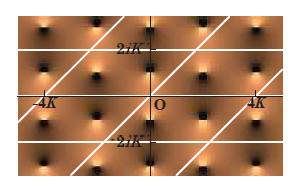
定義域を複素数まで拡張すると, 楕円関数は二重周期性をもつ関数です。 楕円積分から, 楕円関数の二重周期性が証明できます。

• 加法則を用い, 楕円関数の定義域は複素数に拡張できる。
• リーマン面に注意し, 楕円積分を調べると二重周期性が導かれる。

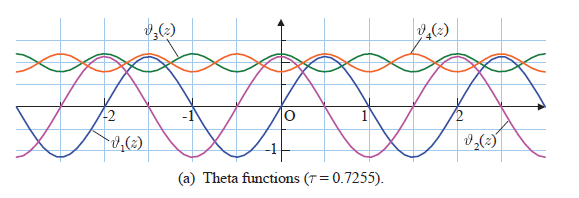
正関数は二重周期をもつことができませんが, 整関数を二つ組み合わせて, 二重周期をとる楕円関数をつくります。その正関数がテータ関数です。 テータ関数自体は整数論で応用されるようですが... (それ以上語れません x_x)

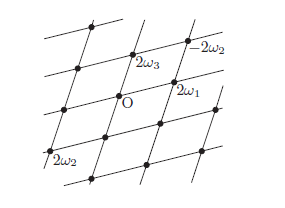
二重周期をもつ基本的な楕円関数として, ワイエルシュトラスの 楕円関数を紹介します。さらに, シグマ関数, コシグマ関数を紹介しますが, 応用分野を含め, しばわんころの理解がいまひとつです。 本章の原稿は, 残念ながら、テキスト受け売りの域を出ていません。

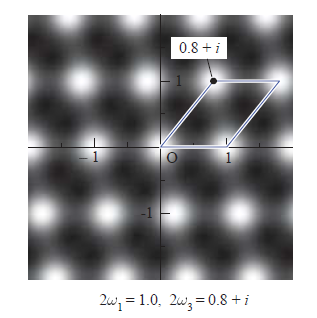
テータ関数からヤコビの楕円関数を計算する公式を導出します。 本章も, しばわんころ が十分に理解できているとはいいがたい状況です。

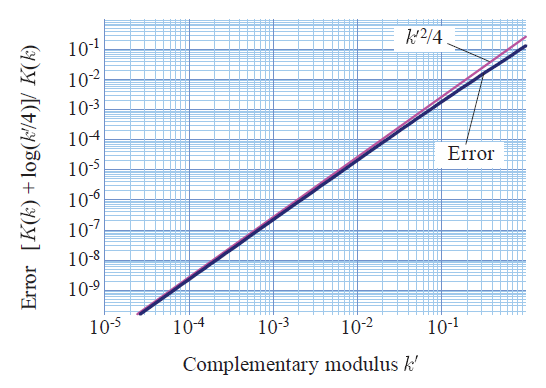
楕円関数は算術幾何平均を用いた高速アルゴリズムに利用されることがあります。 本章では, 円周率と自然対数を多倍長演算するための楕円関数応用について 説明します。

• ガウス・ルジャンドル法の証明と, そのアルゴリズムの効果を説明。
• ガウス・ルジャンドル法は反復するたびに有効数字が2倍になる。
• 自然対数も算術幾何平均で高速演算できる。