連続体の物理学

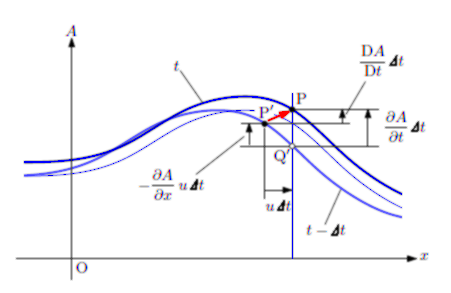
まだまだ, 書き方がかなり雑です。

連続体を数学記述するための二つの方法を説明します。 一つはオイラー記述、もう一方はラグランジュ記述です。 その後, 連続体としての基本方程式となる流れの方程式を解説します。

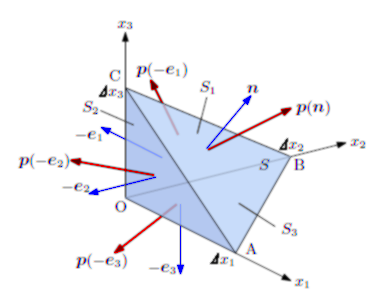
連続体は力を受けると, 明示的に運動するだけでなく, 変形という現象を起こします。本章はそのための基本概念と 数学記述を説明します。

• 力には、体積力と面積力がある。
• 面積力として, 応力がある。応力は, 接線方向と法線方向に分けられる。 圧力や張力は応力の一種。
• 一般の応力を伴う運動方程式はテンソルを使って記述する。

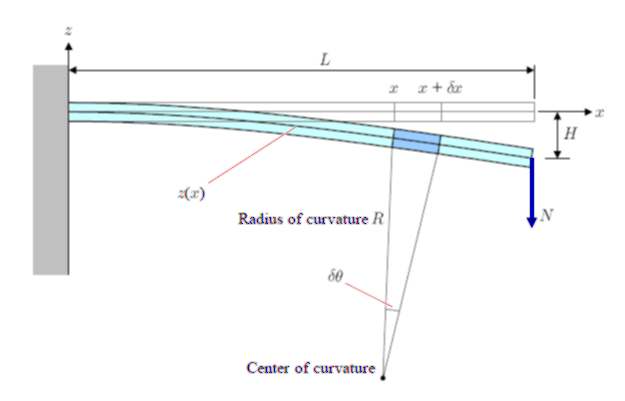
伸び/縮みや曲げなどの変形を取り扱います。 応用例として, 構造体の強度計算である梁の変形を解析します。

• 歪みは伸縮歪みとずれ歪みに分類される。
• 変形の解析には力のモーメントを利用する。
• 集中荷重の片持ち梁について, 梁は3次関数を描いて変形する。
• 両もち梁は片持ち梁より10倍以上強い。

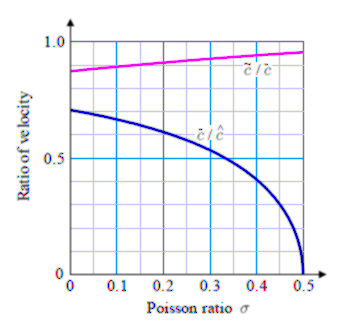
弾性体の動的な変化は波として周囲に伝搬します。 その有名な例が地震波です。 地震波において, 縦波は横波より伝搬速度が速く, 振幅が小さいことは経験的に知られています。 その事実は, 本章で理論的に説明されるのです。

• 弾性波の伝搬方程式は複雑。 よく見ると, 縦波と横波の方程式に分けられる。
• 縦波は疎密波であり, 横波は変形波である。
• 縦波は横波に比べ, 伝搬速度が速く, 振幅が小さい。
• 媒質境界では, 表面はなるややこしい波が存在する。

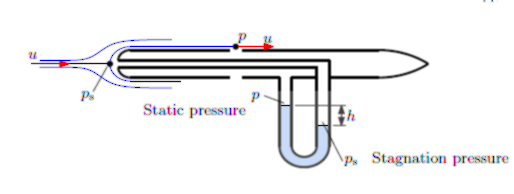
流体は自由に形を変形できる連続体です。 その性質ゆえに, 静止状態では接線応力が存在しません。 運動すると, 速度勾配に応じて接線応力が発生します。 それが, 流体中を運動するときの抵抗になります。

• 流体中の運動方程式は, (当然だが) 連続体の運動方程式から導出される。
• 航空機の対気速度を測るピトー管はベルヌーイの定理の応用。

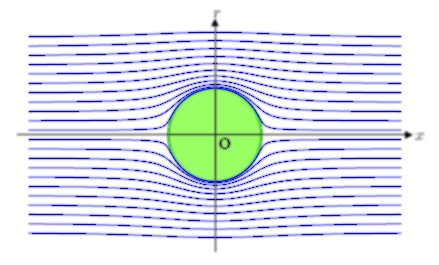
流体の流れは, 流体自体が運動・伝搬することによる流れだけでなく, 単に, 位相が伝搬する波動が存在します。 流れを解析するために, ポテンシャル流の考え方が重要になります。

• ポテンシャル流を利用すると, 簡単なモデルならば流線がきれいに描ける。
• 流体中を運動する物体の運動エネルギーは, 誘導質量分のエネルギーが加算される。
• 乱流を伴う運動にはレイノルズ数に注意。

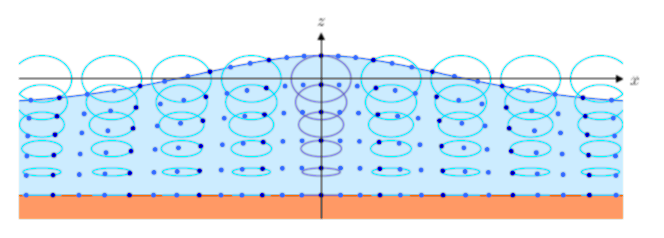
弾性波と同様, 流体も変形と復元が波として周囲に伝搬します。 その例が海面波のような水の波です。 水の波といっても, 津波のような長波や, 一般の海面派のような短波では 性質が大きく異なります。

• 津波のような長波は, 海底でも水が動いている。 水分子の運動軌跡は楕円形。
• 海面波のような短波では, 水面付近しか水は動かない。 水分子の運動軌跡は円形。

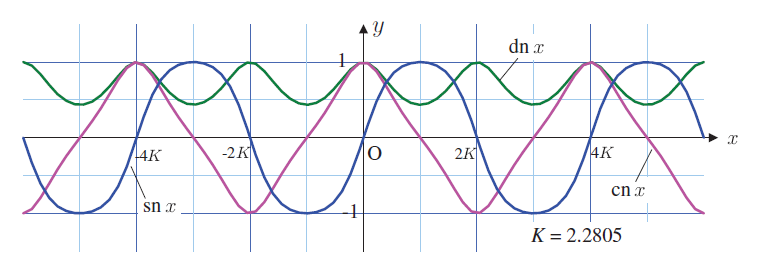
付録A: 楕円積分と楕円関数