一般力学・解析力学

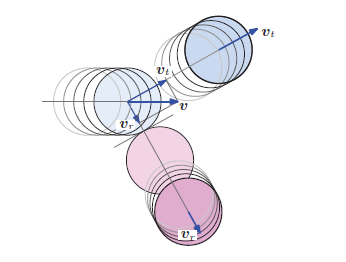
ニュートンの運動方程式をはじめ, 力学の基礎を取り扱います。 本章では運動方程式, 力学的エネルギー保存則, 運動量保存則を 説明していきます。

• 慣性の法則, 運動方程式, 作用反作用の原理で あらゆる力学現象が説明できる。
• ニュートンの記述は, 力を適切に分解することが肝心。
• 保存則 (エネルギー, 運動量) は現象解析に有効なツール。

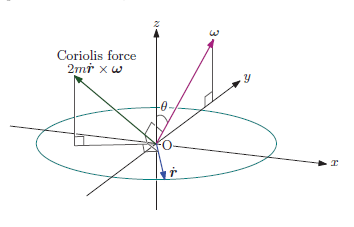
第1章での議論を引き継ぎ, 典型的な運動の解析をしていきます。 特に, 遠心力やコリオリの力のような慣性力をしっかりと 説明しています。

• 運動方程式で, ケプラーの法則が証明できる。
• ケプラー法則に斥力対応しラザフォード散乱を解析する。
• 台風の渦巻きは地球の自転によるコリオリ力が原因。
• フーコーの振り子は地球が自転している証拠。
• 解析する問題は, 自由度が小さいほど好ましい。

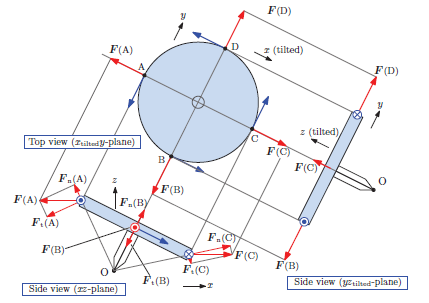
変形しない質点の集合体として, 剛体の運動を取り扱います。 とは言いつつも, 本章でもっとも取り扱いたかったものは回転運動です。 歳差運動するコマの運動にも言及していきます。

• 剛体の自由度は6である。
• 角運動量, 力のモーメントは回転を扱うツール。
• コマが倒れない理由は慣性力。

この章から解析力学です。座標系に関わらず共通の数学記述をするため 座標, 運動量, 力の (数学的) 一般化をはかります。 その一般化の結果, ラグランジュの運動方程式が得られますが, さまざまな恩恵が得られます。

• ラグランジュの運動方程式は, なりふりに構わず, 数学形式を追求した方程式。
• ラグランジアンさえ定義できれば, 力を洗い出さなくても 力学現象を解析でいる。
• ローレンツ力は回転する座標系の運動に類似している。

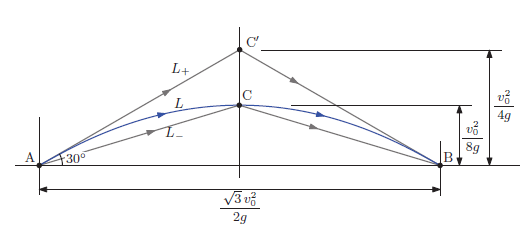
ラグランジュの運動方程式は変分法における最小化問題の解法でした。 そこで作用積分を定義し, 最小作用の原理が提唱されます。 さらには, 座標や時間における対称性が保存則と結びつくという, 驚くべき性質が導かれます。

• ラグランジュの運動方程式は最小化問題の解だった。
• 運動エネルギーの時間積分 (作用積分) を最小化するように 運動経路が決まる。
• 最小作用の原理は, 光学におけるフェルマの原理に相当。
• 力学の対称性は保存則と関係あり。

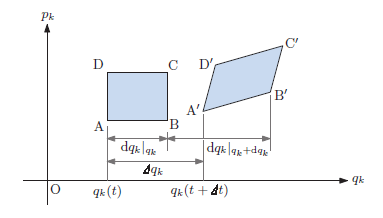
これぞ解析力学に神髄です。 いかに解析する座標成分を減らすか(循環座標をつくるか)のように, 数学形式にこだわって座標, 運動量(位相空間)の変換について 議論していきます。

• 全エネルギーに相当する形式としてハミルトニアンを定義。
• 運動の記述は, 座標と運動量の組み合わせ (位相空間) を使う。
• ポアソン括弧で力学の本質に迫る。
• 正準変換で循環座標をあぶり出す。

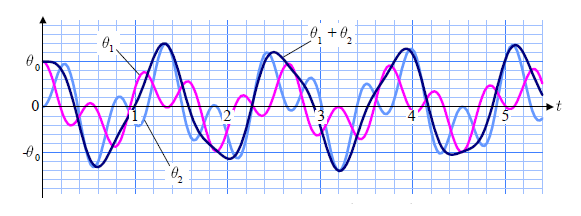
解析力学の応用として複数の質点が振動する系を取り扱います。 振動する質点が術つなぎになっている系は, 作用する力の特定が厄介なため ニュートン記述が難しいです。解析力学では力の特定をしなくても運動方程式が 書けるので, このような問題で効果を発揮します。

• 基本は二重振り子の問題。
• 複数の振動が存在する問題は永年方程式が常套手段。
• 応用例その1: 二酸化炭素の分子運動を解析する。
• 応用例その2: 格子振動から連続体の振動へ。