特殊関数

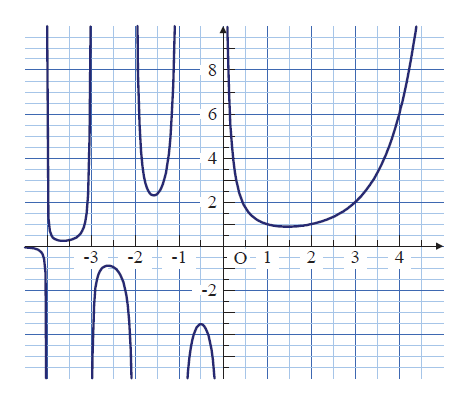
階乗の定義域の拡張としてガンマ関数が定義されます。ガンマ関数への 拡張によって, 大きな変数における階乗が比較的簡単な式で 評価できるようになります。つまり, スターリングの公式です。 スターリングの公式は, 大きな数における組み合わせ数を取り扱う 統計力学で力を発揮します。

• 階乗を整数以外に拡張しようという興味からガンマ関数が誕生した。
• 無限乗積によるガンマ関数の表現と, 任意変数の関数値。
• スターリングの公式で巨大な数の階乗が計算できる。
• 不完全ガンマ関数と指数積分。

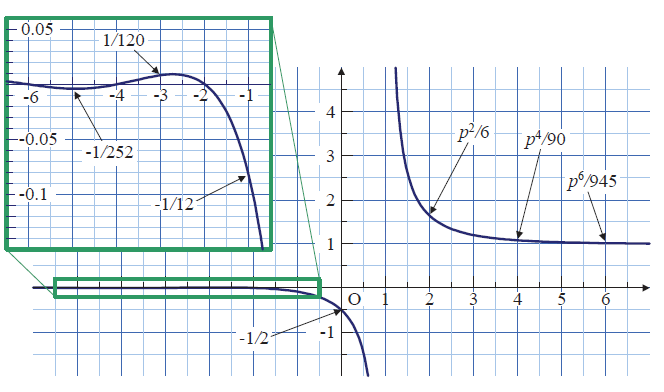
高次の調和級数によって定義されるゼータ関数はガンマ関数と 密接な関係があります。本章での展開にはガンマ関数が用いられます。 また, ガンマ関数は素数とも深い関係があります。物理学においては, 関数としてよりも, γ(2) や γ(4) のように特定の ガンマ関数値が定数として現れることが多いです。

• 調和級数とオイラー定数 γ の関係。
• バーゼル問題: 2次の調和級数は π²/6 に収束する。
• ゼータ関数の導入。偶数ゼータ関数はベルヌーイ数と円周率で記述できる。
• ゼータ関数の解析接続。 1 + 2 + 3 + 4 + ··· = -1/12 ???

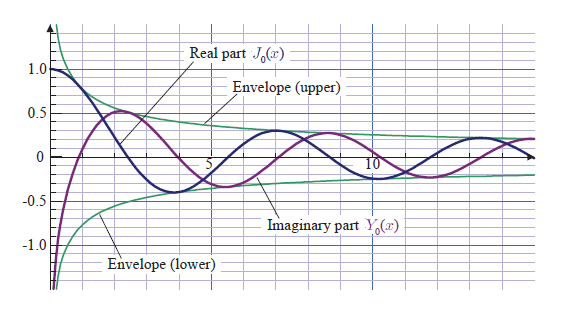
ベッセル関数は円筒座標系における波動関数の解として用いられることが 多いですが, 実は, ケプラーの法則の解として惑星の軌道計算のために 導入されました。本章では, ケプラーの法則の解としての導入から, 変形ベッセル関数までを取り扱います。

• 歴史的なベッセル関数の導入はケプラーの法則の解だった。
• ベッセル関数が満たす微分方程式は円筒座標系の波動方程式に対応する。
• ベッセル関数の正体は, 級数展開によって探る。
• ベッセル関数とノイマン関数, さらに, 複素表現によってハンケル関数へ。
• 微分方程式を少し変形し, 変形ベッセル関数が導入される。

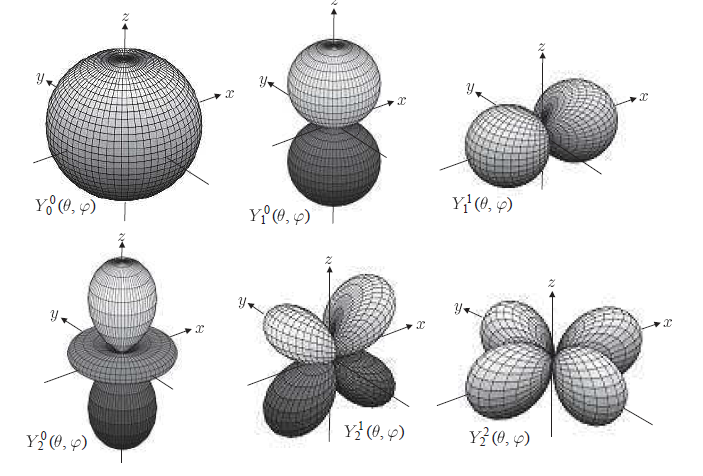
ルジャンドル関数は量子力学での水素原子モデルにおいて, 天頂角依存性を示す関数として登場します。一般的な意味としては, 多重極子を表す関数です。多重極子の性質をもてばルジャンドル関数が 現れるので, 量子力学だけでなく, 電磁放射における天頂角依存性としても 現れます。

• ルジャンドル微分方程式の解としてルジャンドル関数を導入。
• ルジャンドル多項式に多重極子としての性質が反映されている。
• 異なる次数のルジャンドル関数は互いに直交する。
• ルジャンドル陪関数から球面調和関数へ。水素原子の軌道角運動量。

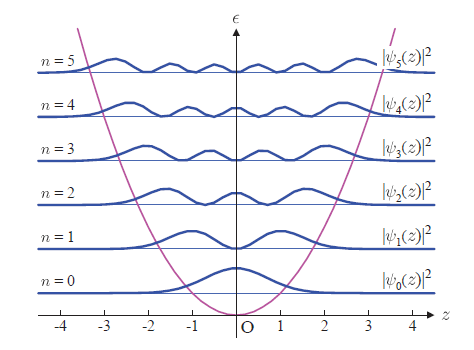
量子力学おける調和振動子としてエルミート関数が導入されました。 調和振動子は基本的なモデルですが, 量子力学における 生成演算子, 消滅演算子のもととなる非常に重要なステップです。 また, エルミート関数は整数次でしか物理的な安定を示さないことが, 量子力学おける「量子」の必然性にしっかりと対応します。

• エルミート微分方程式の解としてエルミート関数の導入。 やはり, スタートは級数展開。
• 整数次でないエルミート関数は無限遠で発散する。 それが, 量子力学の量子性に対応する。
• 調和振動子モデルでは, 整数次のエルミート関数はとびとびの エネルギー順位に対応する。

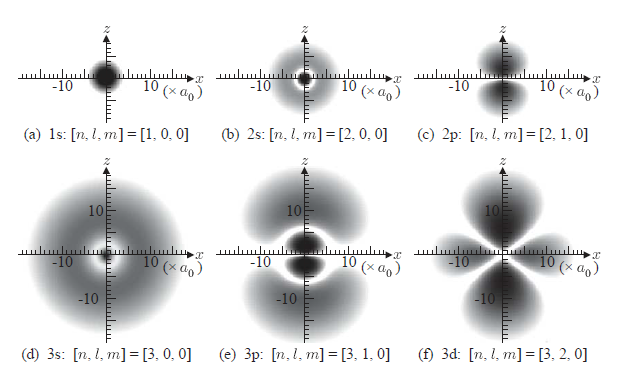
ラゲール関数は量子力学の水素原子モデルにおいて, 動径方向依存性の 関数として用いられます。

• ラゲール微分方程式の解としてのラゲール関数の導入。 性質を調べるには, まず, 級数展開から。
• ラゲールの陪関数と水素原子モデル。 エネルギー順位は, 古典力学モデルと一致する。
• 水素原子の電子は特定の軌道を描かない。 電子の位置は, 電子雲という名の確率密度にしたがう。

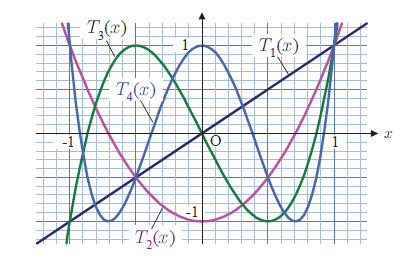
コンピュータにおける近似計算においてチェビシェフ多項式を用いると, 定義域の中で著しい誤差の増大を防ぐことができます。このように, 数値計算でのテクニックとして使用されるチェビシェフ多項式は, 物理学で登場することはほとんどないかもしれません。

• ゲーゲンバウアー多項式からチェビシェフ多項式の導入。
• チェビシェフ多項式の直交性は三角関数の直交性と類似している。
• チェビシェフ多項式による関数の近似。最小誤差はテイラー級数に かなわないが, 誤差が定義域全体で安定している。

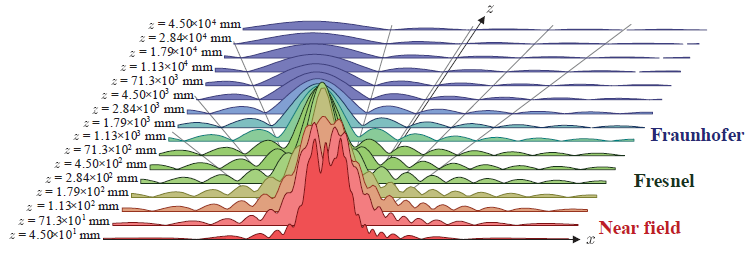
初等関数や特殊関数を積分し, 新たな関数を定義すると, 物理学や工学における問題の解を記号によって記述できます。 本章では, 物理学や工学で頻繁に表れる問題の解法として関数を導入し, それらの性質を調べていきます。

• 誤差関数と逆誤差関数。ガンマ関数と密接な関係がある。
• マーカムのQ関数。雑音に埋もれる信号を抽出する確率を計算できる。
• フレネル積分。光の解析パターン, アンテナの指向性パターンなどを描く。