特殊相対性理論

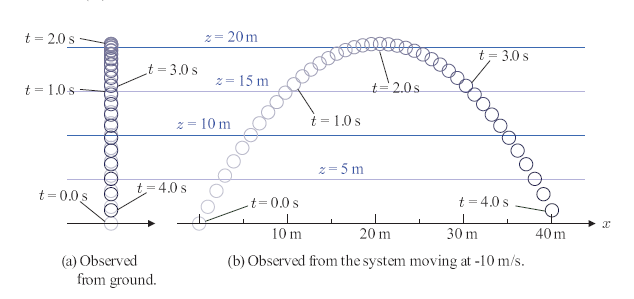
ガリレイの相対性原理, ガリレイ変換から始め, 「相対的である」を 数学で表現するとどうなるか, を最初に示します。その数学表現を利用し, マクスウェルの方程式が ガリレイ変換に対して相対的でないことを示します。

• 相対的であるとは, 物理の基本方程式が不変である。
• マクスウェルの方程式はガリレイ変換のもとで相対的でない。
• マイケルソン・モーレーの実験で発見された光速の謎。
• マクスウェルの方程式は, ローレンツ変換のもとで相対的になる。

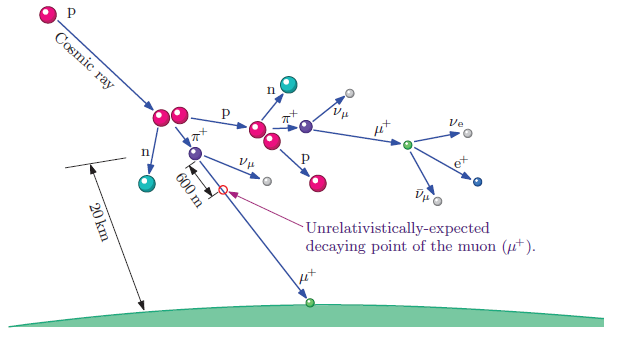
マイケルソン・モーレーの実験結果を「光速不変の原理」として受け入れ, アインシュタイン流の相対性原理を考察すると, ローレンツ変換が 導かれます。その結果, 運動する者の時計がゆっくり進み, ものさしが縮むという, いわゆる, ローレンツ収縮が予言されます。

• 光速不変の原理からローレンツ変換が導出できる。
• 宇宙全体の共通時間は存在しない。
• 運動する者の時計はゆっくり進み, ものさしは縮む。
• ローレンツ変換は虚数角度による座標回転である。

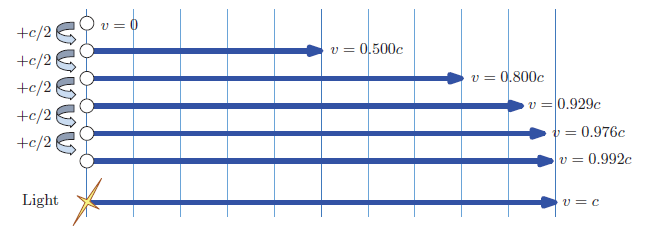
本章のメイントピックはあの有名な公式 E = mc² の導出です。 慣性系の間で力や運動量などを変換することが, そのための準備となります。 相対論では, 空間と時間が切り離せないように, 運動量とエネルギーの間も 密接な関係があります。

• どんなに加速しても光速を超えられない。
• 等加速度運動の相対論的記述。
• 任意運動の運動エネルギーにおけるE = mc²の導出。
• 運動量とエネルギーのローレンツ変換。

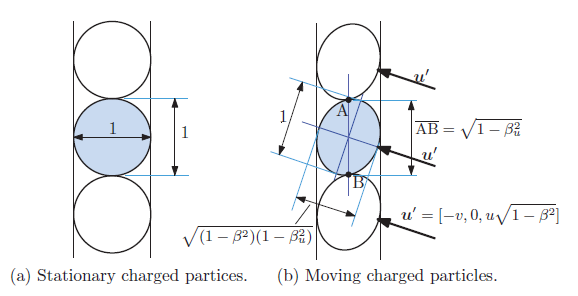
既に確認したように, ローレンツ変換のもとでマクスウェルの方程式は 慣性系の間で相対的です。この性質を利用すると, 磁場の存在が 相対論的効果であることがわかります。

• 電磁場のローレンツ変換。
• 磁場は相対論的効果。
• 運動する誘電体の中では D = εE は成立しない。
• 相対論的な電磁放射。

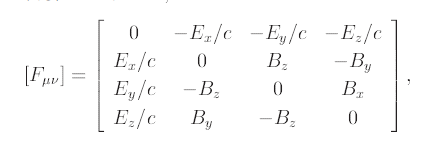
テンソル解析でこれまでの座標変換が容易に導出できることを説明します。 最初にテンソル解析をざっくりと説明した後で, 物理量をテンソル解析に適した形に書き換え, 座標変換が簡単に 記述できることを示します。

• テンソル記法になれる。アインシュタインの総和の規約。
• 物理量の4元ベクトルとしての表記。必ずしも, 物理量をそのまま ベクトルに並べるだけではない。
• 電磁場のテンソル表記とマクスウェル方程式のテンソル記述。